The famous paper An
elementary proof of the prime
nuber theorem, A. Selberg, Annals of Mathematics 50 (1949), pp.303-313
The English
translation of the paper M. Riesz Sur l’hypothese de Riemann,
Acta Mathematica, pp.185-190 v.40 (1916),
originally published in French.
I was really impressed when I read about the electromechanical
device constructed by B. van der Pol in the forties of last
century
which plotted Riemann zeta function on critical line, here is the
original image (zeros are marked by ticks "|" under t axis):
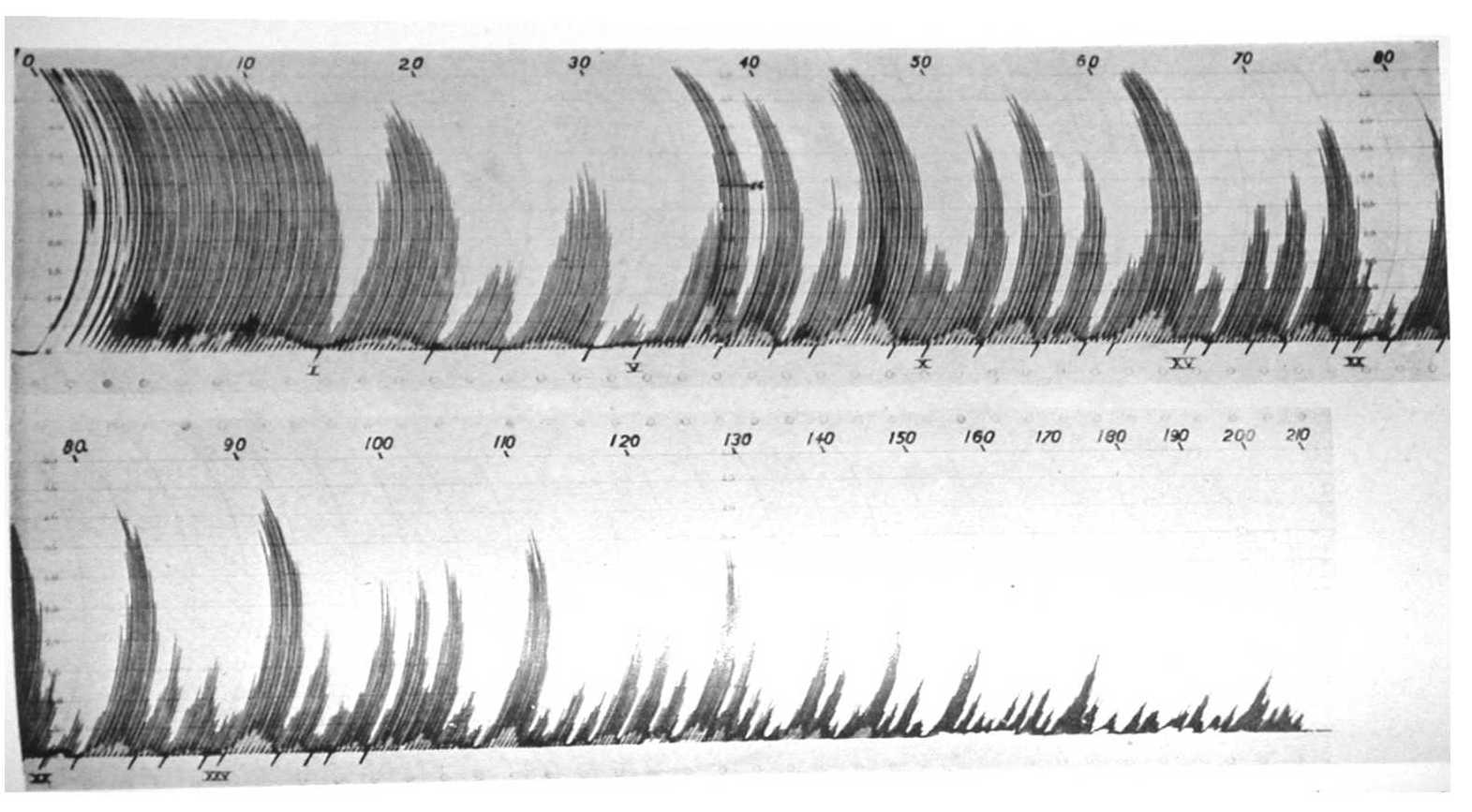
The paper
appeared as An
electro-mechanical investigation of the Riemann zeta function in
the critical strip", Bulletin of the AMS 53
(1947) pp. 976-981
The
pdf file of the famous paper "A Proof
that Euler Missed... Apery's
Proof of the Irrationality of zeta(3)" by Alfred van der
Poorten.
Classical paper G.H. Hardy and
J.E. Littlewood Contributions to the
theory of the Riemann zeta function and the theory of prime distribution Acta
Mathematica 41 (1918) p.119
as a pdf
(9 MB) or djvu
(0.6 MB) file. To display
djvu files the DjVu Browser is needed and it is available
for free from here.
Two famous papers written
by Skewes where he obtained estimation of vaule
of such x that 
for the first time: Skewes, S. On
the Difference [pi(x)-li(x)] J. London Math. Soc. 8,
277-283, 1933 as pdf
(3.8 MB) or as djvu
(only 150 kB) (the paper just before it "Statement of a problem in
quantum mechanics" was written by P.A.M. Dirac) and the second paper
Skewes, S. On the Difference
[pi(x)-li(x)]. II.
Proc. London Math. Soc. 5, 48-70, 1955 as pdf
(11 MB) or as djvu
(400 kB).
E.C. Titchmarsh, The zeros of the Riemann zeta-function,
Proceedings of the
Royal Society of London, volume 151, pages
234-255, 1935. The djvu
file is only 0.2 MB instead of 8 MB for pdf
file.
Here is the pdf file (13 MB) of
the paper "The Roots
of Trigonometric Integrals" Duke Math. J. 17,
197-226, 1950, written over fifty years ago by N.G. de Bruijn
which
opened a new way of proving or disproving The Riemann Hypothesis. It
leads to the notion of de
Bruijn - Newman constant 
, which
should be less or equal to zero if RH is true (and reverse: if RH is
true then is less or equal
0). As the best lower bound is now > -
2.7x10-9 we can say that RH is true up
to 
where
currently < 2.7x10-9.
It lead Odlyzko to say that "if RH is true, it is barely true",
see his paper
An
improved bound for the de Bruijn-Newman constant, which appeared in
Numerical Algorithms, 25 (2000), pp. 293-303
You
can download the djvu file
of the above paper The Roots of
Trigonometric Integrals which
is only 0.3 MB in size (instead of 13 MB for pdf !!!). To display
djvu files the DjVu Browser is needed and it is available
for free from here.